1. The function \(y=\sin x\) is one-to-one on \(\left [ -\dfrac<\pi >,\dfrac<\pi > \right ]\) ; thus, this interval is the range of the inverse function of \(y=\sin x\), \(f(x)=\sin^x\) The function \(y=\cos x\) is one-to-one on \([0,\pi ]\) ; thus, this interval is the range of the inverse function of \(y=\cos x\), \(f(x)=\cos^x\)
3. \(\dfrac<\pi >\) is the radian measure of an angle between \(-\dfrac<\pi >\) and \(\dfrac<\pi >\) whose sine is \(0.5\).
5. In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval \(\left [ -\dfrac<\pi >,\dfrac<\pi > \right ]\) so that it is one-to-one and possesses an inverse.
7. True . The angle, \(\theta _1\) that equals \(\arccos(-x)\), \(x>0\), will be a second quadrant angle with reference angle, \(\theta _2\), where \(\theta _2\) equals \(\arccos x\), \(x>0\). Since \(\theta _2\) is the reference angle for \(\theta _1\), \(\theta _2=\pi - \theta _1\) and \(\arccos(-x)=\pi - \arccos x-\)add texts here. Do not delete this text first.
\( \bigstar \) Evaluate the expressions.
Answers to odd exercises.\( \bigstar \) Use a calculator to evaluate each expression. Express answers to the nearest hundredth.
Answers to odd exercises.37. \(1.98\) 39. \(1.41\) 41. \(0.73\)
\( \bigstar \) Evaluate without a calculator.
45. \(\sin^\left(\sin \left( \dfrac<\pi> \right)\right)\)
46. \(\sin^\left(\sin \left( \dfrac<2\pi> \right)\right)\)
47. \(\sin^\left(\sin \left( \dfrac<5\pi> \right)\right)\)
48. \(\sin^\left(\sin \left( -\dfrac<9\pi> \right)\right)\)
49. \(\sin^\left(\sin \left( -\dfrac<3\pi> \right)\right)\)
50. \(\sin^\left(\sin \left( -\dfrac<\pi> \right)\right)\)
51. \(\cos^\left( \cos \left( \dfrac<\pi> \right)\right)\)
52. \(\cos^\left( \cos \left( \dfrac<17\pi> \right)\right)\)
53. \(\cos^\left( \cos \left( \dfrac<2\pi> \right)\right)\)
54. \(\cos^\left( \cos \left( -\dfrac<11\pi> \right)\right)\)
55. \(\cos^\left( \cos \left( -\dfrac<4\pi> \right)\right)\)
56. \(\cos^\left( \cos \left( -\dfrac<\pi> \right)\right)\)
57. \(\tan^\left(\tan \left( \dfrac<2\pi> \right)\right)\)
58. \(\tan^\left(\tan \left( \dfrac<3\pi> \right)\right)\)
59. \(\tan^\left(\tan \left( \dfrac<17\pi> \right)\right)\)
60. \(\tan^\left(\tan \left( -\dfrac<11\pi> \right)\right)\)
61. \(\tan^\left(\tan \left( -\dfrac<9\pi> \right)\right)\)
62. \(\tan^\left(\tan \left( -\dfrac<4\pi> \right)\right)\)
Answers to odd exercises.\( \bigstar \) Evaluate without a calculator.
65. \(\sin \left(\sin^ \left( \dfrac \right)\right)\)
66. \(\cos \left(\cos^ \left( \dfrac \right)\right)\)
67. \(\tan \left(\tan^ \left( 4 \right) \right) \\[6pt]\)
68. \(\sin \left(\sin^ (-5) \right)\)
69. \(\cos \left(\cos^ \left( -\dfrac \right)\right)\)
70. \(\tan \left(\tan^ \left( -\dfrac \right)\right)\)
Answers to odd exercises.65. \(\dfrac\) \(\qquad\) 67. \( 4 \) \(\qquad\) 69. undefined
\( \bigstar \) Evaluate without a calculator.
72. \(\sin \left(\cos^ \left( \dfrac \right)\right)\)
73. \(\sin \left(\cos^ \left(\dfrac \right)\right)\)
74. \(\sin \left(\tan^ \left(\dfrac \right)\right)\)
76. \(\sin \left(\tan^ \left( 1 \right)\right)\)
77. \(\cos \left(\sin^ \left( \dfrac \right)\right)\)
78. \(\cos \left(\sin^ \left(\dfrac \right)\right)\)
79. \(\cos \left(\tan^ \left(\dfrac \right)\right)\)
80. \(\cos \left(\tan^ \left( -\dfrac \right)\right)\)
84. \(\cot \left(\cos^ \left( \dfrac> \right)\right)\)
85. \(\cot \left(\sin^ \left( \dfrac> \right)\right)\)
86. \(\sec \left(\tan^ \left( -\dfrac \right)\right)\)
87. \(\sec\left(\sin^ \left( -\dfrac \right)\right)\)
88. \(\csc \left(\tan^ \left( \dfrac> \right)\right)\)
89. \(\csc \left(\cos^ \left( \dfrac> \right)\right)\)
| 90. Find the exact value of \(\dfrac\left ( \tfrac \right )-\cos^\left ( \tfrac<\sqrt> \right )+\sin^\left ( \tfrac> \right )-\cos^(1)><\cos^\left ( \tfrac> \right )-\sin^\left ( \tfrac<\sqrt> \right )+\cos^\left ( \tfrac \right )-\sin^(0)>\) |
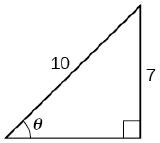
\( \bigstar \) Find the angle \(\theta\) in the given right triangle. Round answers to the nearest hundredth.

102.
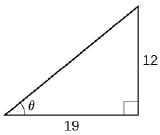
103.
\( \bigstar \) Find the exact value, if possible, without a calculator, or round to the nearest hundredth.
104. \(\sin^\left(\cos \left( \dfrac<2\pi> \right)\right)\)
105. \(\sin^\left(\cos \left(\dfrac<-\pi> \right)\right)\)
107. \(\sin^\left(\tan \left( - \dfrac<4\pi> \right)\right)\)
108. \(\cos^\left(\sin \left(\dfrac<\pi> \right)\right)\)
109. \(\cos^\left(\sin \left( \dfrac<7\pi> \right)\right)\)
110. \(\cos^ \left( \sin \left(\dfrac<5\pi> \right) \right) \)
111. \(\cos^\left(\cot \left( -\dfrac<3\pi> \right)\right)\)
112. \(\tan^\left(\sin \left(\dfrac<4\pi> \right)\right)\)
113. \(\tan^\left(\sin \left(\dfrac<\pi> \right)\right)\)
115. \(\tan^\left(\sin \left(-\dfrac<5\pi> \right)\right)\)
116. \(\tan^\left( \csc \left( \dfrac<7\pi> \right)\right)\)
117. \(\tan^\left( \sec \left( -\dfrac<\pi> \right)\right)\)
Answers to odd exercises.103. \(0.56\) radians 105. \(0\) 107. undefined 109. \( \dfrac<3\pi> \)
111. \(0\) 113. \(0.71\) 115. \(-\dfrac<\pi>\) 117. \( 0.86 \)
For the exercises below, (a) Find the exact value of the expression in terms of \(u\). (b) State any restrictions to \(u\).
121. \(\cos \left( \sin^ \left( u\right)\right)\)
122. \(\tan \left( \sin^ \left( u\right)\right)\)
123. \(\sin \left( \tan^ \left( u\right)\right)\)
124. \(\cos \left( \tan^ \left( u\right)\right)\)
125. \(\tan \left( \cos^ \left( u\right)\right)\)
126. \(\sin \left( \cos^ \left( u\right)\right)\)
127. \(\tan \left(\sin^ (u-1)\right)\)
128. \(\cos \left(\sin^ (1-u)\right)\)
129. \(\cos \left(\sin^ \left(\dfrac\right)\right)\)
130. \(\tan \left(\sin^ \left(\dfrac\right)\right)\)
131. \(\sin \left(\tan^ \left(u+\dfrac\right)\right)\)
132. \(\cos \left(\tan^ (3u-1)\right)\)
133. \( \sin \left( \tan^ \left(\dfrac>\right) \right)\)
Answers to odd exercises.121. \( \sqrt \), \( -1 \le u \le 1 \) 123. \( \dfrac > \), no restrictions 125. \( \dfrac<\sqrt> \), \( -1 \le u \le 1 \)
127. \(\dfrac>\), \( 0 \le u \le 2 \) 129. \(\dfrac>\), \( u \ge 1 \) or \( u \le -1 \) 131. \(\dfrac>>>\), no restrictions
133. \(\dfrac\), \( u \gt -\dfrac \)
138. Graph \(y=\sin^ x\) and state the domain and range of the function.
139. Graph \(y=\arccos x\) and state the domain and range of the function.
140. Graph one cycle of \(y=\tan^ x\) and state the domain and range of the function.
Answers to odd exercises.
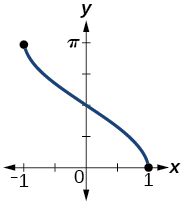
139. domain \([-1,1]\) ; range \([0,\pi ]\)
143. Suppose a \(13\)-foot ladder is leaning against a building, reaching to the bottom of a second-floor window \(12\) feet above the ground. What angle, in radians, does the ladder make with the building?
144. Suppose you drive \(0.6\) miles on a road so that the vertical distance changes from \(0\) to \(150\) feet. What is the angle of elevation of the road?
145. An isosceles triangle has two congruent sides of length \(9\) inches. The remaining side has a length of \(8\) inches. Find the angle that a side of \(9\) inches makes with the \(8\)-inch side.
146. Without using a calculator, approximate the value of \(\arctan (10,000)\) . Explain why your answer is reasonable.
147. A truss for the roof of a house is constructed from two identical right triangles. Each has a base of \(12\) feet and height of \(4\) feet. Find the measure of the acute angle adjacent to the \(4\)-foot side.
148. The line \(y=\dfracx\) passes through the origin in the \(x,y\)-plane. What is the measure of the angle that the line makes with the positive \(x\)-axis?
149. The line \(y=\dfracx\) passes through the origin in the \(x,y\) -plane. What is the measure of the angle that the line makes with the negative \(x\)-axis?
150. What percentage grade should a road have if the angle of elevation of the road is \(4\) degrees? (The percentage grade is defined as the change in the altitude of the road over a \(100\)-foot horizontal distance. For example a \(5\%\) grade means that the road rises \(5\) feet for every \(100\) feet of horizontal distance.)
151. A \(20\)-foot ladder leans up against the side of a building so that the foot of the ladder is \(10\) feet from the base of the building. If specifications call for the ladder's angle of elevation to be between \(35\) and \(45\) degrees, does the placement of this ladder satisfy safety specifications?
152. Suppose a \(15\)-foot ladder leans against the side of a house so that the angle of elevation of the ladder is \(42\) degrees. How far is the foot of the ladder from the side of the house?
Answers to odd exercises.
143. \(0.395\) radians 145. \(1.11\) radians 147. \(1.25\) radians 149. \(0.405\) radians
151. No. The angle the ladder makes with the horizontal is \(60\) degrees..
6.1e: Exercises - Inverse Trigonometric Functions is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.